Inter-rater reliability and inter-coder agreement in ATLAS.ti

- Introduction
- Understanding inter-coder reliability
- The mechanics of inter-coder reliability
- Methodologies for assessing inter-coder reliability
- Strategies to improve inter-coder reliability
- Overcoming common challenges in achieving inter-coder reliability
- Using ATLAS.ti for measuring inter-rater reliability
In qualitative research projects conducted by multiple researchers, inter-coder reliability is a standard reliability measure to ensure a research audience of the degree to which the analysis applied to qualitative data is consistent. This article aims to unpack this essential concept and its significance in the context of qualitative studies, providing you with the insights and strategies needed to enhance the quality and credibility of your research.

In a nutshell, inter-coder reliability refers to the degree of agreement or consistency between two or more coders who are independently coding a set of data. By achieving a high degree of inter-coder reliability, researchers can significantly enhance the trustworthiness and rigor of their qualitative research findings. This becomes especially important in projects where multiple researchers are coding the data separately, each bringing in their unique perspectives and interpretations.
This guide is not merely about explaining what inter-coder reliability is, but more importantly, about why it is a cornerstone in qualitative research where multiple researchers are involved. It's a measure that adds weight to your findings, showing that they aren't the result of one person's interpretation, but a collective agreement reached among multiple coders.
By the end of this article, you will gain a thorough understanding of the concept of inter-coder reliability, its different methodologies for assessment, and strategies to achieve high agreement among coders. We'll explore real-world case studies, offer practical lessons on how to implement these strategies in your own research, and navigate any challenges that might come your way.
This guide aims to be a valuable resource, whether you're a seasoned qualitative researcher or just starting on your research journey. Ensuring inter-coder reliability is no small task, but with the right knowledge and tools, it can significantly bolster the integrity and impact of your research findings.
Understanding inter-coder reliability
Some aspects of qualitative research can be considered relatively more objective in nature. A content analysis of a set of text, for example, can tell you how many times a particular word appears in that set. While the meaning of the data may be subjective, the frequencies produced in a content analysis are not in terms of establishing a set structure for the data. Conversely, coding is a human process that involves a degree of subjective judgment that ultimately differs from person to person. If you have multiple coders looking at the data, demonstrating some measure of consistency or reliability of the coding can persuade your research audience that the codes and the subsequent analysis are credible.

Inter-coder reliability, while a seemingly complex term, can be broken down into two key components. 'Inter-coder' refers to the process involving multiple coders who are independently analyzing and interpreting a dataset. 'Reliability' refers to the level of consistency or agreement that these coders have achieved in their coding. When combined, inter-coder reliability is all about measuring the extent of agreement or consensus among different coders who have worked on the same data set.
The need for inter-coder reliability emerges from the very nature of qualitative research. Qualitative data, whether it's textual, audio, or visual, is often laden with subtleties and nuances. When multiple coders are tasked with making sense of this data, it's not uncommon for them to come up with slightly different interpretations. This is where inter-coder reliability comes in – it ensures that despite the variations in interpretations, there is a reasonable level of agreement among the coders.
It's also important to keep in mind that this is a separate concept from intra-coder reliability, which addresses the consistency of an individual coder who might change their mindset while coding hundreds or even thousands of data segments over an extended period of time. While that is an important concept to consider for establishing research rigor, this article deals with the level of consistency that multiple coders share among each other.
Inter-coder reliability vs. inter-rater reliability
It's also helpful to differentiate inter-coder reliability from a similar concept known as inter-rater reliability. The latter is a statistical measure used primarily in quantitative research to assess the level of agreement among different raters or judges who are scoring a particular dataset. This dataset could be a series of test scores, responses to a survey collecting nominal data or interval data, or ratings of a particular trait or behavior.

Inter-coder reliability, on the other hand, is more specific to qualitative research, where the 'coding' process involves categorizing or labeling data rather than scoring or rating it. The coding process in qualitative research is complex and multi-layered, and it can involve analytic processes such as thematic analysis or grounded theory methodologies. Given the interpretive nature of this coding process, achieving inter-coder reliability can be important to demonstrate the clarity and communicability of the coding system. In reality, both inter-coder and inter-rater reliability are often used interchangeably, but it can be helpful to understand the roots of each in research.
Why inter-coder reliability matters
The importance of inter-coder reliability in maintaining the quality of qualitative research cannot be understated. A high level of inter-coder reliability helps ensure that the findings of the research are not merely a product of one coder's subjective interpretation but are rather a reflection of a collective consensus among multiple coders.

Moreover, inter-coder reliability adds a layer of credibility and trustworthiness to your research. It shows that the coding process has been rigorous and standardized, and the findings can therefore be seen as more reliable. Without inter-coder reliability, the risk of bias or misinterpretation can significantly increase.
Inter-coder reliability also supports the principle of 'transferability' in qualitative research. Transferability refers to the extent to which the findings of one study can be applied or transferred to other contexts or studies. When there is a high level of agreement among different coders who have analyzed the same data, it increases the robustness of the coding system and its potential to be utilized by other researchers in their own studies.
Finally, inter-coder reliability plays a significant role in enhancing the transparency of your research. By clearly documenting the coding process, including how the codes were developed and applied, and how discrepancies among coders were resolved, researchers can provide a clear trail of evidence that supports their findings.

In essence, inter-coder reliability is an essential safeguard against the risks associated with the inherent subjectivity of qualitative research. While this subjectivity is often embraced as a unique strength of qualitative methodologies, other researchers that stem from more quantitative backgrounds may raise concerns with this subjectivity. Inter-coder reliability then offers a way for qualitative researchers to effectively communicate with quantitative researchers and reviewers about the quality of the analysis process. It adds rigor, enhances trustworthiness, supports transferability, and increases transparency. Later in this guide, we will explore how you can effectively achieve inter-coder reliability in your research and the various methodologies and strategies that can help you in this endeavor.
The mechanics of inter-coder reliability
Understanding inter-coder reliability begins with coding, a critical procedure where researchers transcribe, assemble and organize the raw data into manageable units that encapsulate the essence of that data. Coding is essentially a bridge that connects the raw data with the researcher's understanding of it, helping them uncover patterns, themes, and concepts that might have otherwise remained obscured.
The process of coding
Coding in qualitative research can take many forms, but it generally involves a series of steps. It starts with familiarizing oneself with the data. This could involve reading through transcripts, watching videos, or listening to audio recordings multiple times until a general understanding of the content is achieved. During this process, initial codes are generated, which involves identifying meaningful segments in the data and assigning labels (codes) to them. These codes represent the basic elements of the raw data that appear noteworthy or relevant to the research question.

The coding process continues with searching for patterns or themes among the initial codes, reviewing these themes, and finally defining and naming them. This iterative process helps researchers make sense of the data and extract meaning from it. It's important to note that the coding process is not strictly linear. Researchers often move back and forth between these steps as they immerse themselves in the data and refine their understanding of it.
Different approaches to coding
There are several approaches to coding in qualitative research, each with its strengths and limitations. Some researchers prefer an inductive approach where codes are generated from the data itself without any predefined schema. This approach is often associated with grounded theory, where the goal is to generate new theories or propositions from the data. On the other hand, some researchers use a deductive approach, where they start with a predefined set of codes or a theoretical framework that guides their coding process. This approach is commonly used in research where the aim is to verify existing theories.

Another approach is a combination of both, which can be seen as a hybrid approach. Here, researchers might start with a set of predefined codes but remain open to creating new codes as they immerse themselves in the data. This approach allows for the flexibility of the inductive approach while also leveraging the focus and direction provided by the deductive approach.
The role of multiple coders
One of the primary ways to ensure inter-coder reliability is by employing multiple coders to analyze the same data. Having multiple coders helps mitigate the risks associated with individual bias, subjectivity, or misinterpretation. Each coder brings their unique perspective to the data, enhancing the richness and depth of the analysis. However, for these diverse perspectives to contribute to the robustness of the research rather than confound it, a high degree of inter-coder reliability must be achieved. In addition, inter-coder reliability helps construct a well-defined coding system that can be effectively used by multiple people.

It's worth noting that the use of multiple coders does not necessarily imply that all coders must agree on all coding decisions. On the contrary, disagreements among coders can provide valuable insights into the data and the coding process. What's important is that these disagreements are discussed, explored, and resolved in a systematic and transparent manner, contributing to the rigor and credibility of the research.
The impact of low inter-coder reliability
Low inter-coder reliability can be a significant concern in qualitative research. It can lead to inconsistent results and undermine the credibility of the research. Furthermore, if the inter-coder reliability is too low, it might indicate problems with the coding process itself. The codes might be poorly defined, the coding instructions might be unclear, or the coders might not be adequately trained. Most importantly, the difference in thinking between multiple can prevent the creation of a clear conceptualization of the research. In such cases, the researchers might need to revisit and refine their coding process.

In conclusion, understanding the mechanics of inter-coder reliability requires a deep dive into the coding process, the different approaches to coding, and the role of multiple coders. By grasping these elements, researchers can better appreciate the importance of inter-coder reliability and the potential consequences of low inter-coder reliability. As we proceed in this guide, we'll explore various strategies and methodologies to measure and enhance inter-coder reliability in qualitative research.
Methodologies for assessing inter-coder reliability
Establishing inter-coder reliability is essential to ensure the validity of qualitative research findings. However, conducting a reliability analysis requires the use of certain statistical techniques that provide a quantifiable measure of the degree of agreement among different coders. Two common measures that you'll come across when studying inter-coder reliability are Cohen's kappa and Krippendorff's alpha. This section will discuss these methods, providing a simple explanation of each and their respective pros and cons.

Common statistical techniques
- Percent agreement: This is the simplest and most intuitive method to calculate inter-coder reliability by determining just the average degree of agreement among coders. It involves counting the number of times the coders agree on the coded data and dividing it by the total number of coding decisions. While this method is easy to compute, it does not take into account the possibility of agreement occurring by chance.
- Cohen's kappa: To overcome the limitations of the percent agreement method, Cohen's kappa was introduced. It not only considers the observed agreement between the coders but also adjusts for agreement that could happen randomly. A kappa value of 1 indicates perfect agreement, while a value of 0 indicates agreement equivalent to chance. Cohen's kappa is widely used due to its relative simplicity and the fact that it takes into account the possibility of chance agreement.
- Krippendorff's alpha: This is another statistical measure used to calculate inter-coder reliability and is considered more robust than Cohen's kappa. Computing Krippendorff's alpha reliability is intended for addressing projects with larger numbers of coders, different scales of measurement, and missing data, which makes it particularly versatile. An alpha value of 1 indicates perfect agreement, a value of 0 indicates the absence of agreement, and a negative value indicates inverse agreement.
Pros and cons of each method
Each of these methods has its strengths and limitations. The percent agreement method, while simple and easy to compute, does not consider the possibility of chance agreement, which can lead to an overestimate of inter-coder reliability.
Cohen's kappa, while more robust than percent agreement, has its limitations too. It works best with two coders and may not be suitable for studies with more coders. Additionally, it does not handle missing data well and assumes that all categories of the coding schema are equally difficult to code, which might not always be the case.
Krippendorff's alpha, on the other hand, can accommodate more than two coders, different scales of measurement, and missing data. However, it's computationally more complex than Cohen's kappa and may not be as intuitively understandable for some researchers.
Examples in action
To understand these concepts better, let's take a simple example. Suppose two coders are coding a set of 10 data points into two categories: A and B. If both coders assign the same category to 8 out of the 10 data points, the percent agreement would be 80%.
To calculate Cohen's kappa, one would also consider the agreement expected by chance. If both coders had a 50% chance of coding a data point as A or B, the chance agreement would be 50%. The kappa statistic would then take into account both the observed agreement (80%) and the expected agreement (50%), providing a measure that adjusts for chance agreement.
On the other hand, to calculate Krippendorff's alpha, one would consider all possible pairs of coding decisions, the disagreement for each pair, and the total observed disagreement. The alpha statistic would then provide a measure of reliability that accounts for the observed disagreement and the expected disagreement.
By understanding these methodologies and how to apply them, researchers can better assess the level of inter-coder reliability in their studies. It's important to choose the methodology that best fits the specifics of your research and the nature of your data. Understanding these concepts will enhance your ability to maintain the rigor and reliability of your qualitative research findings.
Strategies to improve inter-coder reliability
Inter-coder reliability helps convey the credibility of qualitative research and facilitates communication with researchers across disciplines. However, as is clear by now, achieving a satisfactory level of this reliability can be quite challenging. This section will take you through various strategies that can be implemented to improve inter-coder reliability in your qualitative research studies.
Developing a clear coding scheme
A comprehensive, well-structured, and clearly articulated coding scheme is the foundation of inter-coder reliability. The coding scheme should detail the different codes, their definitions, and examples of when and how to apply them. Ambiguity in the coding scheme can lead to discrepancies in coding, and consequently, low inter-coder reliability. Therefore, it's key to ensure that each code is distinctly defined, and there is minimal overlap between different codes.
Training the coders
Even the most meticulously crafted coding scheme can fall short if the coders aren't adequately trained. The training should familiarize the coders with the nature of the data, the objectives of the research, and the coding scheme. The training can involve several practice sessions where the coders code a subset of the data and discuss their coding decisions. This collaborative exercise can help uncover any misunderstandings or confusion regarding the coding scheme and refine it before actual coding begins.

Regular meetings and discussions
Throughout the coding process, it's helpful to have regular meetings where the coders can discuss their coding decisions, resolve disagreements, and seek clarifications. These meetings can serve as a platform for mutual learning and continuous refinement of the coding process. Additionally, discussing the coding decisions can enhance the understanding and interpretation of the data, contributing to the richness of the research findings.

Pilot testing the coding scheme
Before plunging into the full-scale coding process, it's advisable to pilot test the coding scheme. This involves coding a small subset of the data and assessing the inter-coder reliability. If the reliability is low, it could indicate issues with the coding scheme or the coding process that need to be addressed. Pilot testing can help identify these issues early on and prevent potential pitfalls in the later stages of the research.
Iterative coding process
The coding process in qualitative research is not a one-time affair. It's an iterative process that involves cycles of coding, reviewing, refining, and recoding. With each cycle, the understanding of the data deepens, the coding scheme becomes more refined, and the level of inter-coder reliability improves. Embracing this iterative nature of the coding process can significantly enhance the quality of your research.

Resolving disagreements systematically
Disagreements among coders are not necessarily a problem – they can provide valuable insights into the data and the coding process. What's important is how these disagreements are resolved. The resolution process should be systematic, transparent, and grounded in the data. It can involve discussions, consultations with a third party, or referring back to the research objectives and the coding scheme. Documenting this process can provide a clear trail of evidence that supports the credibility of the research.
Utilizing software tools
There are numerous software tools like ATLAS.ti that can aid in the coding process and the assessment of inter-coder reliability. These tools can automate the calculation of reliability statistics such as Krippendorff's alpha, making the process more efficient. Moreover, some tools offer features that support collaborative coding, which can be particularly beneficial in studies involving multiple coders.

Ultimately, improving inter-coder reliability is a multifaceted task that involves clear communication, rigorous training, systematic resolution of disagreements, and continuous refinement of the coding process. By implementing these strategies, you can enhance the reliability, credibility, and overall quality of your qualitative research. However, remember that inter-coder reliability is not just about achieving high agreement among coders. It's also about understanding and embracing the complexity of the data, the diversity of interpretations, and the inherent subjectivity of qualitative research. After all, it's this richness and depth that make qualitative research such a powerful tool for understanding the world around us.
Overcoming common challenges in achieving inter-coder reliability
Qualitative researchers are likely to encounter a variety of challenges in achieving inter-coder reliability. These challenges may include issues related to the complexity of the data, the subjectivity of the coding process, or the logistics of coordinating with multiple coders. In this section, we will look at some of these common challenges and provide practical strategies for overcoming them.
Complexity and ambiguity of the data
Qualitative data often involves rich, complex, and nuanced narratives that can be open to multiple interpretations. This complexity can pose a challenge to achieving inter-coder reliability, as different coders may perceive and interpret the data in different ways. One way to address this issue is to invest in a rigorous training process that familiarizes the coders with the nuances of the data and the research objectives. Additionally, having regular discussions and debriefing sessions can help align the coders' understanding and interpretation of the data.
Subjectivity of the coding process
In qualitative research, the coding process is inherently subjective. The coders bring their perspectives, assumptions, and interpretations to the data, which can influence their coding decisions. It's important to establish clear, understandable criteria for each code in the coding scheme. The coders should also be encouraged to reflect on their interpretations and assumptions and consider how these might influence their coding.
Multiple coders with diverse backgrounds
When multiple coders with diverse backgrounds are involved in a study, achieving inter-coder reliability can become more challenging. Different coders might bring different cultural, disciplinary, or experiential lenses to the data, which can lead to discrepancies in coding. However, this diversity can also be a strength, as it can lead to a richer, more comprehensive understanding of the data. To incorporate this diversity in your research while also ensuring reliability, it's important to foster open communication, mutual respect, and a culture of learning among the coders.

Time and resource constraints
Achieving inter-coder reliability can be a time-consuming and resource-intensive process. It involves training the coders, developing and refining the coding scheme, coding the data, assessing reliability, resolving disagreements, and possibly recoding the data. For researchers working under tight deadlines or with limited resources, these requirements can pose a significant challenge. To address this issue, researchers can utilize software tools that automate some aspects of the coding and reliability assessment process. Additionally, careful planning and management of the research process can help optimize the use of resources. In addition, to assess the clarity of the coding system, it can be sufficient to have others code only a subset of the data and measure the inter-coder agreement to refine the coding system where any discrepancies are identified.
Maintaining consistency over time
In long-term research projects, maintaining consistency in the coding process over time can be a challenge. As the research progresses, the coders might subtly shift their understanding or interpretation of the codes, leading to inconsistencies in the coding. To mitigate this risk, it's helpful to have regular review sessions where the coders revisit the coding scheme and the coded data and check for consistency.
Resolving disagreements
Disagreements among coders are almost inevitable in qualitative research. However, these disagreements can sometimes be difficult to resolve, especially when the coders have strong, differing opinions. To overcome this challenge, it's important to establish a systematic and transparent process for resolving disagreements. This could involve discussions, third-party consultations, or referring back to the research objectives and the coding scheme.

Achieving inter-coder reliability in qualitative research is undoubtedly a challenging task, but it's not an insurmountable one. By anticipating these challenges and implementing strategies to overcome them, researchers can enhance the reliability, credibility, and overall quality of their research. Moreover, striving for inter-coder reliability is not just about ensuring consistency among coders. It's also an opportunity for researchers to deepen their understanding of the data, refine their research methods, and engage in a meaningful, collaborative research process.
Using ATLAS.ti for measuring inter-rater reliability
As mentioned previously, computer-assisted qualitative data analysis software is an essential tool for measuring agreement within a qualitative project team. Researchers can collaborate on coding data in ATLAS.ti, then merge projects together to view and analyze the differences in coding to determine the extent of agreement among the coders.
In a project that requires collaboration, the researcher who is considered the project leader distributes copies of the project to different coders. Each copy shares the same documents and codes for each coder to work on. When each coder has completed their coding, they return the completed project to the project leader, who then merges the projects together. The fully-merged project shows all of the different applications of coding, which can be displayed in ATLAS.ti.
Take a look at the screenshot showing a set of sample data below. In our example, two different coders have coded a document with the code "Ethics of consumption." The two coders' application of the code looks very similar, but there are very small but noticeable differences that will be picked up in a full reliability analysis. The first coder appears to have coded entire paragraphs, while the second coder has stopped short of applying the code to the whole of two of the paragraphs. Intuitively, we can guess that the two coders are "close enough" to each other to be consistent. However, if a rigorous analysis is required, ATLAS.ti can provide a reliability measure for coding in this project.
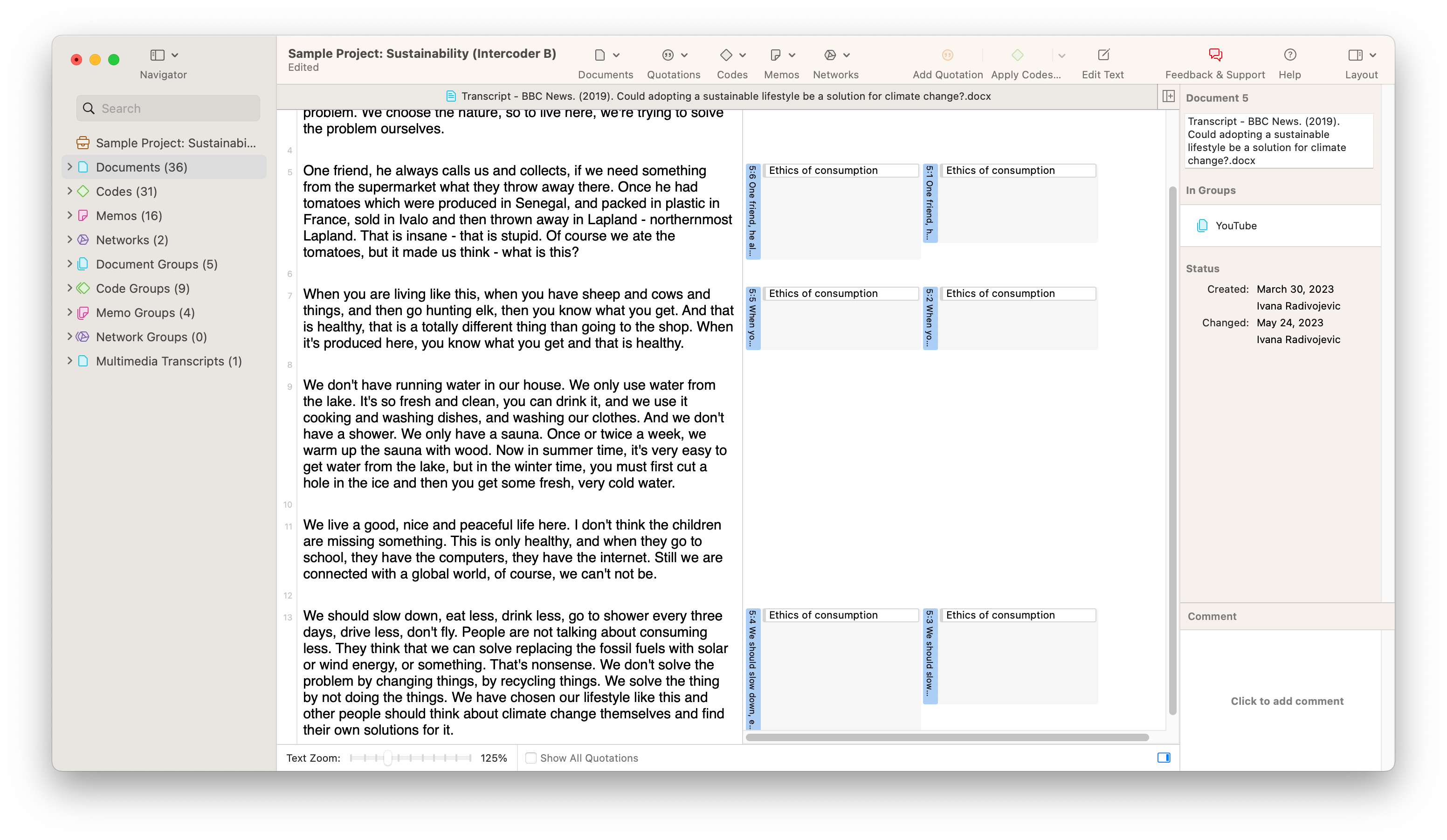
ATLAS.ti calculates reliability among different coders with the Intercoder Agreement tool. This is a simple matter of choosing which documents have been coded, which coders have examined the data, and which codes have been applied to the data. In the screenshot below, you will find the differences in coding visualized on two horizontal bars representing the data being analyzed. The numbers next to each horizontal bar represent the proportion of the data that has been coded with the selected code or codes that make up the semantic domain being analyzed. You can analyze these numbers to get a sense of how much each coder has coded. Moreover, you can choose which agreement measure to use to determine inter-coder agreement.
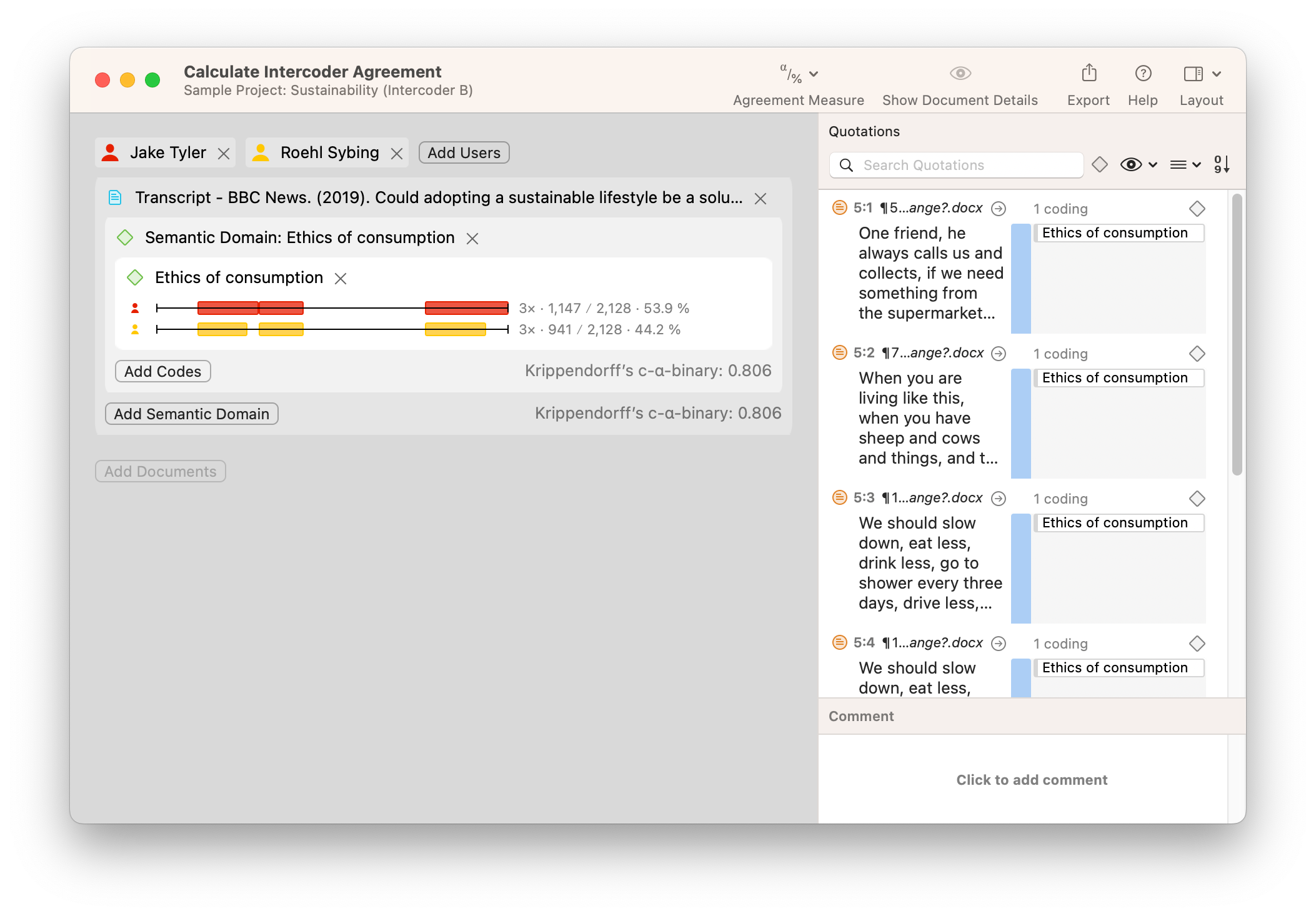
How you interpret data coding differences is up to you. Does the value of agreement meet a necessary minimum threshold? Do any of the differences suggest important discrepancies that merit revisiting the code definitions? As with many tools in ATLAS.ti, the results that are produced are just the first step in making judgments and interpretations about your data; it is up to you to use the results to persuade your audience regarding what the data means.