Fiabilidad entre evaluadores y acuerdo entre codificadores en ATLAS.ti

En los proyectos de investigación cualitativa realizados por múltiples investigadores, la fiabilidad entre codificadores es una medida de fiabilidad estándar para garantizar al público investigador el grado de coherencia del análisis aplicado a los datos cualitativos. Este artículo pretende desentrañar este concepto esencial y su importancia en el contexto de los estudios cualitativos, proporcionándole las ideas y estrategias necesarias para mejorar la calidad y credibilidad de su investigación.

En pocas palabras, la fiabilidad entre codificadores se refiere al grado de acuerdo o coherencia entre dos o más codificadores que codifican independientemente un conjunto de datos. Al alcanzar un alto grado de fiabilidad entre codificadores, los investigadores pueden aumentar significativamente la fiabilidad y el rigor de los resultados de su investigación cualitativa. Esto es especialmente importante en los proyectos en los que varios investigadores codifican los datos por separado, aportando cada uno sus propias perspectivas e interpretaciones.

Esta guía no se limita a explicar qué es la fiabilidad entre codificadores, sino, lo que es más importante, por qué es una piedra angular en la investigación cualitativa en la que participan varios investigadores. Es una medida que añade peso a los hallazgos y demuestra que no son el resultado de la interpretación de una sola persona, sino de un acuerdo colectivo alcanzado entre varios codificadores.

Al final de este artículo, comprenderá en profundidad el concepto de fiabilidad entre codificadores, sus diferentes metodologías de evaluación y las estrategias para lograr un alto grado de acuerdo entre codificadores. Exploraremos estudios de casos reales, ofreceremos lecciones prácticas sobre cómo implementar estas estrategias en su propia investigación y sortearemos cualquier desafío que pueda surgir.

Esta guía pretende ser un recurso valioso, tanto si es un investigador cualitativo experimentado como si acaba de iniciar su andadura en la investigación. Garantizar la fiabilidad entre codificadores no es tarea fácil, pero con los conocimientos y las herramientas adecuadas puede reforzar significativamente la integridad y el impacto de los resultados de la investigación.

Comprender la fiabilidad entre codificadores

Algunos aspectos de la investigación cualitativa pueden considerarse relativamente más objetivos por naturaleza. Un análisis de contenido de un conjunto de textos, por ejemplo, puede indicar cuántas veces aparece una palabra determinada en ese conjunto. Aunque el significado de los datos puede ser subjetivo, las frecuencias producidas en un análisis de contenido no lo son en términos de establecer una estructura fija para los datos. Por el contrario, la codificación es un proceso humano que implica cierto grado de juicio subjetivo que, en última instancia, difiere de una persona a otra. Si son varios los codificadores que examinan los datos, demostrar cierta coherencia o fiabilidad en la codificación puede convencer al público de que los códigos y el análisis posterior son creíbles.

Inter-coder reliability, while a seemingly complex term, can be broken down into two key components. 'Inter-coder' refers to the process involving multiple coders who are independently analyzing and interpreting a dataset. 'Reliability' refers to the level of consistency or agreement that these coders have achieved in their coding. When combined, inter-coder reliability is all about measuring the extent of agreement or consensus among different coders who have worked on the same data set.

The need for inter-coder reliability emerges from the very nature of qualitative research. Qualitative data, whether it's textual, audio, or visual, is often laden with subtleties and nuances. When multiple coders are tasked with making sense of this data, it's not uncommon for them to come up with slightly different interpretations. This is where inter-coder reliability comes in – it ensures that despite the variations in interpretations, there is a reasonable level of agreement among the coders.

It's also important to keep in mind that this is a separate concept from intra-coder reliability, which addresses the consistency of an individual coder who might change their mindset while coding hundreds or even thousands of data segments over an extended period of time. While that is an important concept to consider for establishing research rigor, this article deals with the level of consistency that multiple coders share among each other.

Inter-coder reliability vs. inter-rater reliability

It's also helpful to differentiate inter-coder reliability from a similar concept known as inter-rater reliability. The latter is a statistical measure used primarily in quantitative research to assess the level of agreement among different raters or judges who are scoring a particular dataset. This dataset could be a series of test scores, responses to a survey collecting nominal data or interval data, or ratings of a particular trait or behavior.

Por otra parte, la fiabilidad entre codificadores es más específica de la investigación cualitativa, en la que el proceso de "codificación" implica categorizar o etiquetar los datos en lugar de puntuarlos o clasificarlos. El proceso de codificación en la investigación cualitativa es complejo y tiene múltiples capas, y puede implicar procesos analíticos como el análisis temático o las metodologías de teoría fundamentada. Dada la naturaleza interpretativa de este proceso de codificación, lograr la fiabilidad entre codificadores puede ser importante para demostrar la claridad y comunicabilidad del sistema de codificación. En realidad, tanto la fiabilidad entre codificadores como la fiabilidad entre evaluadores suelen utilizarse indistintamente, pero puede ser útil comprender las raíces de cada una de ellas en la investigación.

Por qué es importante la fiabilidad entre codificadores

No se puede subestimar la importancia de la fiabilidad entre codificadores para mantener la calidad de la investigación cualitativa. Un alto nivel de fiabilidad entre codificadores ayuda a garantizar que los resultados de la investigación no sean meramente el producto de la interpretación subjetiva de un codificador, sino más bien el reflejo de un consenso colectivo entre múltiples codificadores.

Además, la fiabilidad entre codificadores añade credibilidad y fiabilidad a la investigación. Demuestra que el proceso de codificación ha sido riguroso y estandarizado, por lo que los resultados pueden considerarse más fiables. Sin fiabilidad entre codificadores, el riesgo de sesgo o interpretación errónea puede aumentar considerablemente.

La fiabilidad entre codificadores también apoya el principio de "transferibilidad" en la investigación cualitativa. La transferibilidad se refiere al grado en que las conclusiones de un estudio pueden aplicarse o transferirse a otros contextos o estudios. Cuando existe un alto nivel de acuerdo entre diferentes codificadores que han analizado los mismos datos, aumenta la solidez del sistema de codificación y su potencial para ser utilizado por otros investigadores en sus propios estudios.

Por último, la fiabilidad entre codificadores desempeña un papel importante en la mejora de la transparencia de su investigación. Al documentar claramente el proceso de codificación, incluida la forma en que se desarrollaron y aplicaron los códigos, y cómo se resolvieron las discrepancias entre codificadores, los investigadores pueden proporcionar un rastro claro de pruebas que respalden sus conclusiones.

En esencia, la fiabilidad entre codificadores es una salvaguarda esencial contra los riesgos asociados a la subjetividad inherente a la investigación cualitativa. Aunque esta subjetividad se suele considerar un punto fuerte de las metodologías cualitativas, otros investigadores que proceden de entornos más cuantitativos pueden plantear dudas al respecto. La fiabilidad entre codificadores ofrece a los investigadores cualitativos una forma de comunicarse eficazmente con los investigadores cuantitativos y los revisores sobre la calidad del proceso de análisis. Añade rigor, mejora la fiabilidad, favorece la transferibilidad y aumenta la transparencia. Más adelante en esta guía, exploraremos cómo puede lograr eficazmente la fiabilidad entre codificadores en su investigación y las diversas metodologías y estrategias que pueden ayudarle en este empeño.

La mecánica de la fiabilidad entre codificadores

La comprensión de la fiabilidad entre codificadores comienza con la codificación, un procedimiento fundamental en el que los investigadores transcriben, reúnen y organizan los datos brutos en unidades manejables que encapsulan la esencia de esos datos. La codificación es esencialmente un puente que conecta los datos brutos con la comprensión que el investigador tiene de ellos, ayudándole a descubrir patrones, temas y conceptos que de otro modo podrían haber quedado oscurecidos.

El proceso de codificación

La codificación en la investigación cualitativa puede adoptar muchas formas, pero generalmente implica una serie de pasos. Empieza por familiarizarse con los datos. Esto puede implicar leer las transcripciones, ver vídeos o escuchar las grabaciones de audio varias veces hasta lograr una comprensión general del contenido. Durante este proceso se generan los códigos iniciales, lo que implica identificar segmentos significativos en los datos y asignarles etiquetas (códigos). Estos códigos representan los elementos básicos de los datos brutos que parecen dignos de mención o relevantes para la pregunta de investigación.

The coding process continues with searching for patterns or themes among the initial codes, reviewing these themes, and finally defining and naming them. This iterative process helps researchers make sense of the data and extract meaning from it. It's important to note that the coding process is not strictly linear. Researchers often move back and forth between these steps as they immerse themselves in the data and refine their understanding of it.

Different approaches to coding

There are several approaches to coding in qualitative research, each with its strengths and limitations. Some researchers prefer an inductive approach where codes are generated from the data itself without any predefined schema. This approach is often associated with grounded theory, where the goal is to generate new theories or propositions from the data. On the other hand, some researchers use a deductive approach, where they start with a predefined set of codes or a theoretical framework that guides their coding process. This approach is commonly used in research where the aim is to verify existing theories.

Otro enfoque es una combinación de ambos, que puede considerarse un enfoque híbrido. En este caso, los investigadores pueden comenzar con un conjunto de códigos predefinidos, pero permanecen abiertos a la creación de nuevos códigos a medida que se sumergen en los datos. Este enfoque permite la flexibilidad del enfoque inductivo al tiempo que aprovecha el enfoque y la dirección que proporciona el enfoque deductivo.

El papel de los codificadores múltiples

Una de las principales formas de garantizar la fiabilidad entre codificadores es emplear varios codificadores para analizar los mismos datos. Contar con varios codificadores ayuda a mitigar los riesgos asociados al sesgo individual, la subjetividad o la interpretación errónea. Cada codificador aporta su perspectiva única a los datos, lo que aumenta la riqueza y profundidad del análisis. Sin embargo, para que estas diversas perspectivas contribuyan a la solidez de la investigación en lugar de confundirla, debe alcanzarse un alto grado de fiabilidad entre codificadores. Además, la fiabilidad entre codificadores ayuda a construir un sistema de codificación bien definido que pueda ser utilizado eficazmente por múltiples personas.

Cabe señalar que el uso de varios codificadores no implica necesariamente que todos ellos deban estar de acuerdo en todas las decisiones de codificación. Al contrario, los desacuerdos entre codificadores pueden aportar información valiosa sobre los datos y el proceso de codificación. Lo importante es que estos desacuerdos se discutan, exploren y resuelvan de forma sistemática y transparente, contribuyendo así al rigor y la credibilidad de la investigación.

El impacto de una baja fiabilidad entre codificadores

La baja fiabilidad entre codificadores puede ser un problema importante en la investigación cualitativa. Puede dar lugar a resultados incoherentes y socavar la credibilidad de la investigación. Además, si la fiabilidad entre codificadores es demasiado baja, puede indicar problemas con el propio proceso de codificación. Los códigos pueden estar mal definidos, las instrucciones de codificación pueden ser poco claras o los codificadores pueden no haber recibido la formación adecuada. Y lo que es más importante, la diferencia de pensamiento entre múltiples puede impedir la creación de una conceptualización clara de la investigación. En estos casos, los investigadores pueden tener que revisar y perfeccionar su proceso de codificación.

En conclusión, para comprender la mecánica de la fiabilidad entre codificadores es necesario profundizar en el proceso de codificación, los distintos enfoques de codificación y el papel de los codificadores múltiples. Al comprender estos elementos, los investigadores pueden apreciar mejor la importancia de la fiabilidad entre codificadores y las consecuencias potenciales de una baja fiabilidad entre codificadores. A medida que avancemos en esta guía, exploraremos diversas estrategias y metodologías para medir y mejorar la fiabilidad entre codificadores en la investigación cualitativa.

Metodologías para evaluar la fiabilidad entre codificadores

Establecer la fiabilidad entre codificadores es esencial para garantizar la validez de los resultados de la investigación cualitativa. Sin embargo, realizar un análisis de fiabilidad requiere el uso de determinadas técnicas estadísticas que proporcionan una medida cuantificable del grado de acuerdo entre los distintos codificadores. Dos medidas comunes que encontrará al estudiar la fiabilidad entre codificadores son el kappa de Cohen y el alfa de Krippendorff. Esta sección profundizará en estos métodos, proporcionando una explicación sencilla de cada uno y sus respectivos pros y contras.

Técnicas estadísticas habituales

1. Porcentaje de acuerdo: Es el método más sencillo e intuitivo para calcular la fiabilidad entre codificadores, ya que sólo determina el grado medio de acuerdo entre ellos. Consiste en contar el número de veces que los codificadores están de acuerdo en los datos codificados y dividirlo por el número total de decisiones de codificación. Aunque este método es fácil de calcular, no tiene en cuenta la posibilidad de que el acuerdo se produzca por casualidad.
2. Kappa de Cohen: Para superar las limitaciones del método del porcentaje de acuerdo, se introdujo la kappa de Cohen. No sólo tiene en cuenta el acuerdo observado entre los codificadores, sino que también ajusta el acuerdo que podría producirse al azar. Un valor kappa de 1 indica un acuerdo perfecto, mientras que un valor de 0 indica un acuerdo equivalente al azar. La kappa de Cohen se utiliza ampliamente debido a su relativa simplicidad y al hecho de que tiene en cuenta la posibilidad de que se produzca un acuerdo fortuito.
3. Alfa de Krippendorff: Es otra medida estadística utilizada para calcular la fiabilidad entre codificadores y se considera más robusta que la kappa de Cohen. El cálculo de la fiabilidad alfa de Krippendorff está pensado para abordar proyectos con un mayor número de codificadores, diferentes escalas de medición y datos que faltan, lo que lo hace especialmente versátil. Un valor alfa de 1 indica un acuerdo perfecto, un valor de 0 indica la ausencia de acuerdo y un valor negativo indica un acuerdo inverso.

Pros y contras de cada método

Cada uno de estos métodos tiene sus puntos fuertes y sus limitaciones. El método del porcentaje de concordancia, aunque sencillo y fácil de calcular, no tiene en cuenta la posibilidad de concordancia fortuita, lo que puede dar lugar a una sobreestimación de la fiabilidad entre codificadores.

El kappa de Cohen, aunque es más sólido que el porcentaje de acuerdo, también tiene sus limitaciones. Funciona mejor con dos codificadores y puede no ser adecuada para estudios con más codificadores. Además, no maneja bien los datos que faltan y asume que todas las categorías del esquema de codificación son igualmente difíciles de codificar, lo que puede no ser siempre el caso.

El alfa de Krippendorff, por otro lado, puede acomodar a más de dos codificadores, diferentes escalas de medida y datos perdidos. Sin embargo, es computacionalmente más complejo que el kappa de Cohen y puede no ser tan intuitivamente comprensible para algunos investigadores.

Ejemplos en acción

Para entender mejor estos conceptos, pongamos un ejemplo sencillo. Supongamos que dos codificadores codifican un conjunto de 10 puntos de datos en dos categorías: A y B. Si ambos codificadores asignan la misma categoría a 8 de los 10 puntos de datos, el porcentaje de acuerdo sería del 80%.

Para calcular el kappa de Cohen, también habría que considerar el acuerdo esperado por azar. Si ambos codificadores tuvieran una probabilidad del 50% de codificar un punto de datos como A o B, el acuerdo por azar sería del 50%. El estadístico kappa tendría en cuenta tanto el acuerdo observado (80%) como el esperado (50%), proporcionando una medida que ajusta el acuerdo por azar.

Por otra parte, para calcular el alfa de Krippendorff, habría que considerar todos los pares posibles de decisiones de codificación, el desacuerdo de cada par y el desacuerdo total observado. El estadístico alfa proporcionaría entonces una medida de fiabilidad que tiene en cuenta el desacuerdo observado y el desacuerdo esperado.

Al comprender estas metodologías y cómo aplicarlas, los investigadores pueden evaluar mejor el nivel de fiabilidad entre codificadores en sus estudios. Es importante elegir la metodología que mejor se adapte a las características específicas de su investigación y a la naturaleza de sus datos. La comprensión de estos conceptos mejorará su capacidad para mantener el rigor y la fiabilidad de los resultados de su investigación cualitativa.

Estrategias para mejorar la fiabilidad entre codificadores

La fiabilidad entre codificadores contribuye a transmitir la credibilidad de la investigación cualitativa y facilita la comunicación con investigadores de distintas disciplinas. Sin embargo, como es evidente a estas alturas, alcanzar un nivel satisfactorio de esta fiabilidad puede ser todo un reto. En esta sección se describen varias estrategias que pueden aplicarse para mejorar la fiabilidad entre codificadores en los estudios de investigación cualitativa.

Desarrollo de un esquema de codificación claro

Un esquema de codificación completo, bien estructurado y claramente articulado es la base de la fiabilidad entre codificadores. El esquema de codificación debe detallar los diferentes códigos, sus definiciones y ejemplos de cuándo y cómo aplicarlos. La ambigüedad en el esquema de codificación puede dar lugar a discrepancias en la codificación y, en consecuencia, a una baja fiabilidad entre codificadores. Por lo tanto, es crucial asegurarse de que cada código esté claramente definido y de que haya un solapamiento mínimo entre los distintos códigos.

Formación de los codificadores

Incluso el esquema de codificación más meticulosamente elaborado puede quedarse corto si los codificadores no reciben la formación adecuada. La formación debe familiarizar a los codificadores con la naturaleza de los datos, los objetivos de la investigación y el esquema de codificación. La formación puede incluir varias sesiones de práctica en las que los codificadores codifiquen un subconjunto de los datos y discutan sus decisiones de codificación. Este ejercicio de colaboración puede ayudar a descubrir cualquier malentendido o confusión en relación con el esquema de codificación y perfeccionarlo antes de que comience la codificación real.

Reuniones y debates periódicos

A lo largo del proceso de codificación, resulta útil celebrar reuniones periódicas en las que los codificadores puedan debatir sus decisiones de codificación, resolver desacuerdos y solicitar aclaraciones. Estas reuniones pueden servir de plataforma para el aprendizaje mutuo y el perfeccionamiento continuo del proceso de codificación. Además, debatir las decisiones de codificación puede mejorar la comprensión y la interpretación de los datos, contribuyendo a la riqueza de los resultados de la investigación.

Prueba piloto del sistema de codificación

Antes de sumergirse en el proceso de codificación a gran escala, es aconsejable realizar una prueba piloto del sistema de codificación. Se trata de codificar un pequeño subconjunto de datos y evaluar la fiabilidad entre codificadores. Si la fiabilidad es baja, podría indicar problemas con el sistema de codificación o el proceso de codificación que hay que resolver. Las pruebas piloto pueden ayudar a identificar estos problemas desde el principio y evitar posibles escollos en las fases posteriores de la investigación.

Proceso de codificación iterativo

El proceso de codificación en la investigación cualitativa no se realiza una sola vez. Es un proceso iterativo que implica ciclos de codificación, revisión, refinamiento y recodificación. Con cada ciclo se profundiza en la comprensión de los datos, se refina el esquema de codificación y mejora el nivel de fiabilidad entre codificadores. Adoptar esta naturaleza iterativa del proceso de codificación puede mejorar considerablemente la calidad de la investigación.

Resolución sistemática de desacuerdos

Los desacuerdos entre codificadores no son necesariamente un problema: pueden aportar información valiosa sobre los datos y el proceso de codificación. Lo importante es cómo se resuelven estos desacuerdos. El proceso de resolución debe ser sistemático, transparente y basado en los datos. Puede incluir discusiones, consultas con terceros o referencias a los objetivos de la investigación y al esquema de codificación. La documentación de este proceso puede proporcionar un rastro claro de pruebas que respalden la credibilidad de la investigación.

Utilización de herramientas informáticas

Existen numerosas herramientas informáticas, como ATLAS.ti, que pueden ayudar en el proceso de codificación y la evaluación de la fiabilidad entre codificadores. Estas herramientas pueden automatizar el cálculo de estadísticas de fiabilidad como el alfa de Krippendorff, haciendo que el proceso sea más eficiente. Además, algunas herramientas ofrecen funciones que permiten la codificación colaborativa, lo que puede ser especialmente beneficioso en estudios en los que participan varios codificadores.

En última instancia, mejorar la fiabilidad entre codificadores es una tarea polifacética que implica una comunicación clara, una formación rigurosa, la resolución sistemática de desacuerdos y el perfeccionamiento continuo del proceso de codificación. La aplicación de estas estrategias puede mejorar la fiabilidad, la credibilidad y la calidad general de la investigación cualitativa. Sin embargo, recuerde que la fiabilidad entre codificadores no consiste sólo en lograr un alto grado de acuerdo entre ellos. También consiste en comprender y aceptar la complejidad de los datos, la diversidad de interpretaciones y la subjetividad inherente a la investigación cualitativa. Al fin y al cabo, son esta riqueza y profundidad las que hacen de la investigación cualitativa una herramienta tan poderosa para comprender el mundo que nos rodea.

Superar los problemas habituales para lograr la fiabilidad entre codificadores

Es probable que los investigadores cualitativos se enfrenten a diversos retos a la hora de lograr la fiabilidad entre codificadores. Estos problemas pueden incluir cuestiones relacionadas con la complejidad de los datos, la subjetividad del proceso de codificación o la logística de coordinación con varios codificadores. En esta sección, examinaremos algunos de estos retos comunes y proporcionaremos estrategias prácticas para superarlos.

Complejidad y ambigüedad de los datos

Los datos cualitativos suelen incluir narraciones ricas, complejas y matizadas que pueden estar abiertas a múltiples interpretaciones. Esta complejidad puede suponer un reto para lograr la fiabilidad entre codificadores, ya que los distintos codificadores pueden percibir e interpretar los datos de maneras diferentes. Una forma de abordar este problema es invertir en un proceso de formación riguroso que familiarice a los codificadores con los matices de los datos y los objetivos de la investigación. Además, la celebración periódica de debates y sesiones informativas puede ayudar a armonizar la comprensión e interpretación de los datos por parte de los codificadores.

Subjetividad del proceso de codificación

En la investigación cualitativa, el proceso de codificación es inherentemente subjetivo. Los codificadores aportan sus perspectivas, suposiciones e interpretaciones a los datos, lo que puede influir en sus decisiones de codificación. Es importante establecer criterios claros y comprensibles para cada código del esquema de codificación. También se debe animar a los codificadores a reflexionar sobre sus interpretaciones y suposiciones y a considerar cómo pueden influir en su codificación.

Varios codificadores con distintas formaciones

Cuando en un estudio participan varios codificadores con distintos antecedentes, puede resultar más difícil lograr la fiabilidad entre codificadores. Los diferentes codificadores pueden aportar diferentes perspectivas culturales, disciplinarias o experienciales a los datos, lo que puede dar lugar a discrepancias en la codificación. Sin embargo, esta diversidad también puede ser un punto fuerte, ya que puede conducir a una comprensión más rica y completa de los datos. Para aprovechar esta diversidad y garantizar al mismo tiempo la fiabilidad, es fundamental fomentar la comunicación abierta, el respeto mutuo y una cultura de aprendizaje entre los codificadores.

Limitaciones de tiempo y recursos

Conseguir la fiabilidad entre codificadores puede ser un proceso que requiera mucho tiempo y recursos. Implica formar a los codificadores, desarrollar y perfeccionar el esquema de codificación, codificar los datos, evaluar la fiabilidad, resolver los desacuerdos y, posiblemente, recodificar los datos. Para los investigadores que trabajan con plazos ajustados o recursos limitados, estos requisitos pueden suponer un reto importante. Para resolver este problema, los investigadores pueden utilizar herramientas informáticas que automatizan algunos aspectos del proceso de codificación y evaluación de la fiabilidad. Además, una planificación y gestión cuidadosas del proceso de investigación pueden ayudar a optimizar el uso de los recursos. Además, para evaluar la claridad del sistema de codificación, puede bastar con que otros codifiquen sólo un subconjunto de los datos y midan la concordancia entre codificadores para perfeccionar el sistema de codificación cuando se identifiquen discrepancias.

Mantener la coherencia a lo largo del tiempo

En los proyectos de investigación a largo plazo, mantener la coherencia del proceso de codificación a lo largo del tiempo puede ser un reto. A medida que avanza la investigación, los codificadores pueden cambiar sutilmente su comprensión o interpretación de los códigos, lo que puede provocar incoherencias en la codificación. Para mitigar este riesgo, es útil celebrar sesiones de revisión periódicas en las que los codificadores vuelvan a examinar el esquema de codificación y los datos codificados y comprueben la coherencia.

Resolución de desacuerdos

Los desacuerdos entre codificadores son casi inevitables en la investigación cualitativa. Sin embargo, a veces pueden ser difíciles de resolver, sobre todo cuando los codificadores tienen opiniones fuertes y divergentes. Para superar este reto, es importante establecer un proceso sistemático y transparente de resolución de desacuerdos. Esto puede implicar discusiones, consultas a terceros o volver a los objetivos de la investigación y al esquema de codificación.

Lograr la fiabilidad entre codificadores en la investigación cualitativa es, sin duda, una tarea difícil, pero no insuperable. Al anticipar estos retos y aplicar estrategias para superarlos, los investigadores pueden mejorar la fiabilidad, la credibilidad y la calidad general de su investigación. Además, esforzarse por conseguir la fiabilidad entre codificadores no consiste sólo en garantizar la coherencia entre ellos. También es una oportunidad para que los investigadores profundicen en su comprensión de los datos, perfeccionen sus métodos de investigación y participen en un proceso de investigación significativo y colaborativo.

Uso de ATLAS.ti para medir la fiabilidad entre evaluadores

Como se ha mencionado anteriormente, el software de análisis de datos cualitativos asistido por ordenador es una herramienta esencial para medir la concordancia dentro de un equipo de proyecto cualitativo. Los investigadores pueden colaborar en la codificación de los datos en ATLAS.ti y, a continuación, fusionar los proyectos para ver y analizar las diferencias en la codificación y determinar el grado de acuerdo entre los codificadores.

En un proyecto que requiere colaboración, el investigador que es considerado el líder del proyecto distribuye copias del proyecto a diferentes codificadores. Cada copia comparte los mismos documentos y códigos para que cada codificador trabaje en ellos. Cuando cada codificador ha terminado de codificar, devuelve el proyecto terminado al jefe de proyecto, que fusiona los proyectos. El proyecto completamente fusionado muestra todas las diferentes aplicaciones de la codificación, que pueden mostrarse en ATLAS.ti.

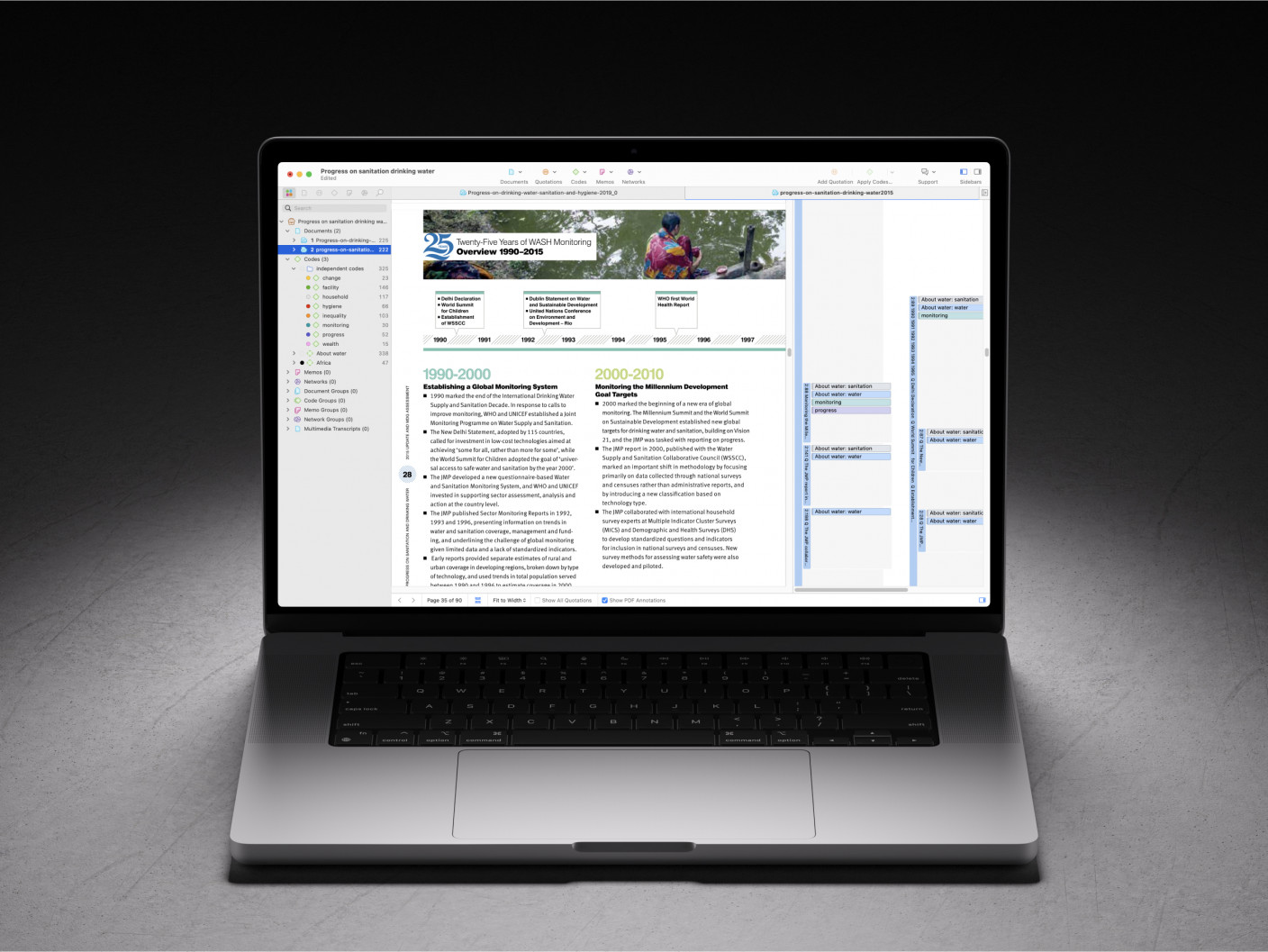
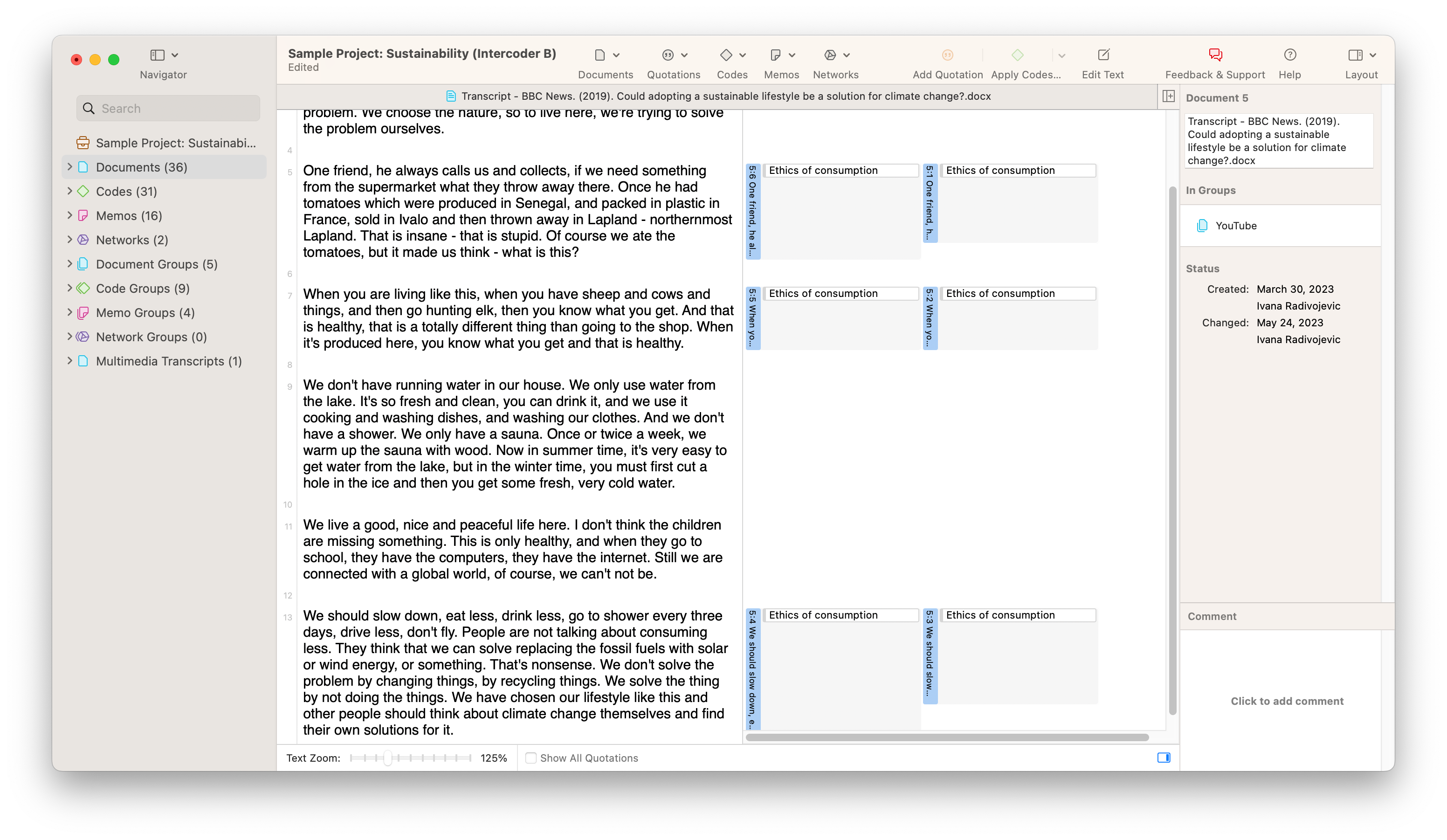
Eche un vistazo a la captura de pantalla que muestra un conjunto de datos de muestra a continuación. En nuestro ejemplo, dos codificadores diferentes han codificado un documento con el código "Ética del consumo". La aplicación del código por parte de los dos codificadores parece muy similar, pero hay diferencias muy pequeñas pero notables que se recogerán en un análisis de fiabilidad completo. El primer codificador parece haber codificado párrafos enteros, mientras que el segundo no ha llegado a aplicar el código a la totalidad de dos de los párrafos. Intuitivamente, podemos suponer que los dos codificadores están lo suficientemente "cerca" entre sí como para ser coherentes. Sin embargo, si se requiere un análisis riguroso, ATLAS.ti puede proporcionar una medida de fiabilidad para la codificación en este proyecto.

ATLAS.ti calcula la fiabilidad entre diferentes codificadores con la herramienta Acuerdo entre Codificadores. Esto es una simple cuestión de elegir qué documentos han sido codificados, qué codificadores han examinado los datos, y qué códigos se han aplicado a los datos. En la siguiente captura de pantalla, encontrará las diferencias de codificación visualizadas en dos barras horizontales que representan los datos analizados. Los números junto a cada barra horizontal representan la proporción de los datos que han sido codificados con el código o códigos seleccionados que componen el dominio semántico analizado. Puede analizar estos números para hacerse una idea de cuánto ha codificado cada codificador. Además, puede elegir qué medida de concordancia utilizar para determinar la concordancia entre codificadores.

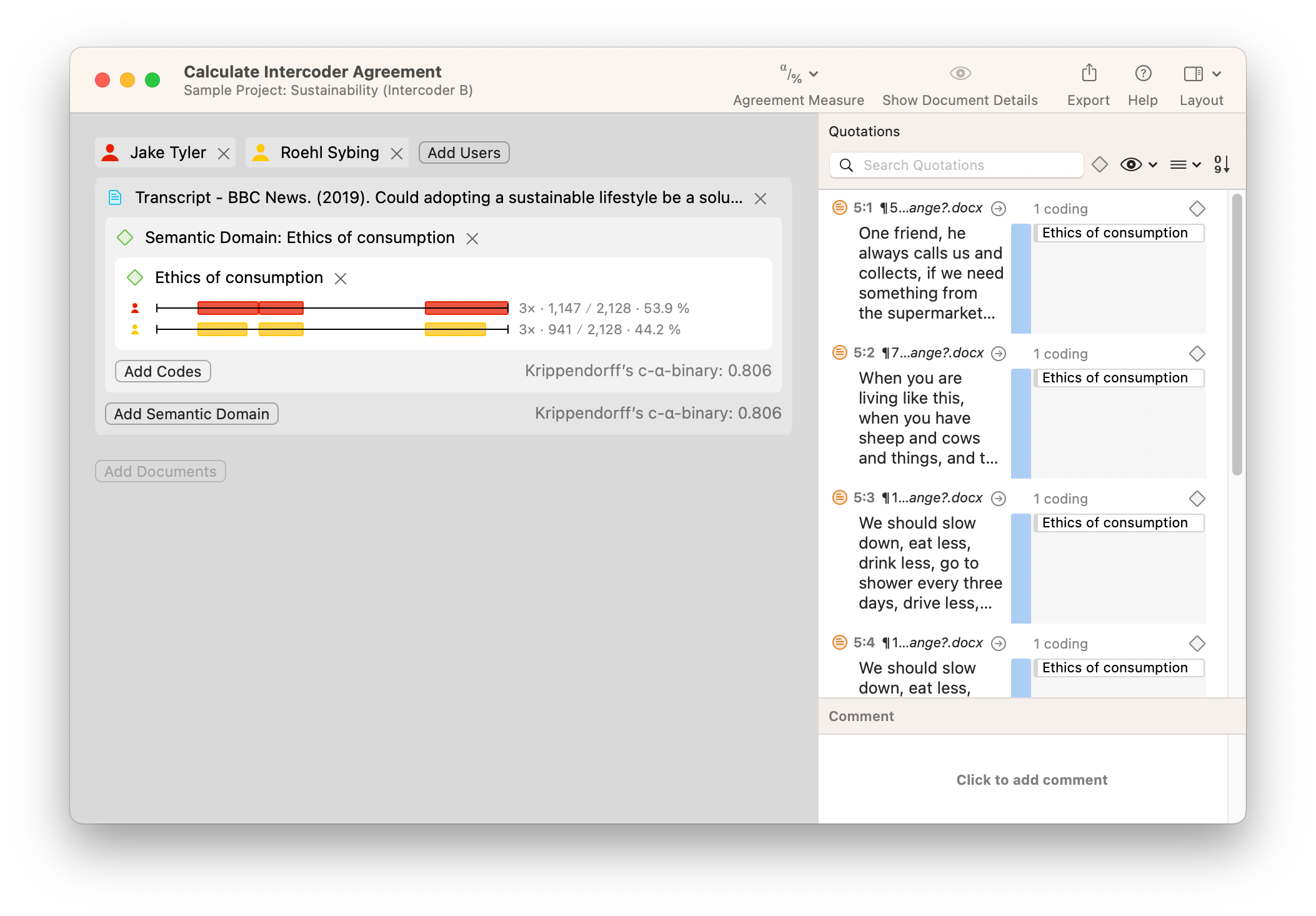
La forma de interpretar las diferencias de codificación de los datos depende de usted. ¿Cumple el valor de concordancia un umbral mínimo necesario? ¿Alguna de las diferencias sugiere discrepancias importantes que merezcan revisar las definiciones de los códigos? Como con muchas herramientas de ATLAS.ti, los resultados que se producen son sólo el primer paso para hacer juicios e interpretaciones sobre sus datos; depende de usted utilizar los resultados para persuadir a su audiencia sobre lo que significan los datos.